Bildungsgänge/Bildungspläne

Beschreibung der Lernsituation

Ein "Quadreieck“ soll als Puzzle aus Holz hergestellt werden.

Wie kann man ein gleichseitiges Dreieck zerschneiden, sodass man aus den Einzelteilen ein Quadrat zusammenlegen kann?

Zielbeschreibung

• Geometrische Flächen konstruieren und berechnen
• Längen- und Flächenberechnungen am Beispiel eines gleichseitigen Dreiecks und eines Quadrates
• Anwendung des Pythagoras
• Detailgenaues Konstruieren und Teilen im gleichseitigen Dreieck
• Herstellung im Fachpraxisunterricht

Hinweise

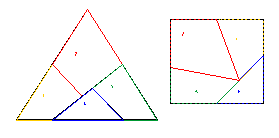
Man sollte den Schülerinnen und Schülern eine angemessene Zeit zur Entwicklung der Lösung für die Aufteilung des Dreiecks gewähren. Nach vergeblichen Bemühungen empfiehlt es sich, die Aufteilung im gleichseitigen Dreieck als Detailkonstruktion vorzustellen. Die Suche nach der richtigen Zusammenstellung der Puzzleteile zu einem Quadrat gestaltet sich als spannende und kreative Auseinandersetzung mit den Grundformen.

Die Aufgabe verbindet die Flächenberechnung und den Satz des Pythagoras mit der Konstruktion- und Arbeitsplanung in sehr einleuchtender Form. Als Ergänzung eignet sich der Zerlegungsbeweis des Pythagoras aus dem 9. Jahrhundert von den Indern.

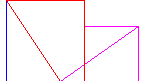
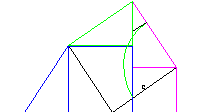
Man erhält das Hypotenusenquadrat durch einfaches Umklappen aus den beiden Kathetenquadraten.

Das "Quadreieck-Puzzle“ eignet sich auch als Grundlage für eine Produktentwicklung: Auftrag: Für der Verkauf ist für das "Quadreieck“ eine geeignete Verpackungs- und Präsentationshülle (ein Kästchen) zu entwerfen und herzustellen.

Für die Fertigung in der Fachpraxis sollen die Schülerinnen und Schüler aus ihren Ausbildungsbetrieben Reste von unterschiedlichen Holzarten mitbringen

Literatur: Beutelspacher, A.: Mathematik zum anfassen. 2. Auflage. Gießen: 2002.